Appearance
回溯算法
回溯算法除了用来指导像深度优先搜索这种经典的算法设计之外,还可以用在很多实际的软件开发场景中,比如正则表达式匹配、编译原理中的语法分析等。
除此之外,很多经典的问题都可以用回溯算法来解决,例如数独,八皇后,0-1背包、图的着色、旅行商问题、全排列等等。
如何理解回溯算法
笼统地讲,回溯算法很多时候都应用在“搜索”这类问题上。不过这里说的搜索,并不是狭义的指图的搜索算法,而是在一组可能的解中,搜索满足期望的解。
回溯的处理思想,有点类似枚举搜索。我们枚举所有的解,找到满足期望的解**。为了有规律地枚举所有可能的解,避免遗漏和重复,我们把问题求解的过程分为多个阶段。每个阶段,我们都会面对一个岔路口,我们先随意选一条路走,当发现这条路走不通的时候(不符合期望的解),就回退到上一个岔路口,另选一种走法继续走。
为了理解,看一个经典的回溯例子,八皇后问题。
有一个 8x8 的棋盘,希望往里放 8 个棋子(皇后),每个棋子所在的行、列、对角线都不能有另一个棋子。八皇后问题就是期望找到所有满足这种要求的放棋子方式。
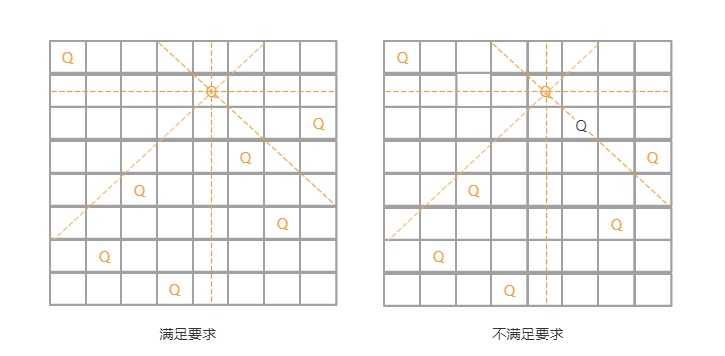
这个问题划分成 8 个阶段,依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的过程中,我们不停地检查当前的方法,是否满足要求。如果满足,则跳到下一行继续放置棋子;如果不满足,那就再换一种方法,继续尝试。
回溯算法非常适合用递归代码实现,把八皇后的算法翻译成代码:
js
let result = new Array(8);
function cal8queue(row) {
if (row === 8) {
console.log(result);
printQueens(result);
return;
}
// 执行所有可能
for (let column = 0; column < 8; column ++) {
if (isOk(row, column)) {
result[row] = column;
cal8queue(row + 1);
}
}
function isOk(row, column) {
// 对角
let leftUp = column - 1;
let rightUp = column + 1;
for (let i = row - 1; i >= 0; i--) { // 逐行往上考察每一行
if (result[i] === column) return false; // // 第i行的 column 列是否有棋子
if (leftUp >= 0) { // 左上对角线,第i行 leftUp 列是否有棋子
if (result[i] === leftUp) return false;
}
if (rightUp <= 8) { // 右上对角线,第i行 rightUp 列是否有棋子
if (result[i] === rightUp) return false;
}
--leftUp;
++rightUp;
}
console.log(row, column);
return true;
}
function printQueens(result) {
let arr = new Array(8).fill([]);
for (let row = 0; row < 8; row++) {
for (let column = 0; column < 8; column++) {
if (result[row] === column) {
arr[row].push('Q');
} else {
arr[row].push('*');
}
}
}
console.log(arr);
}
}
cal8queue(0);
经典应用
回溯算法的理论知识很容易弄懂,比较难的是用递归来实现。
0-1 背包
0-1 背包问题有很多变体,这里一种比较基础的:
有一个背包,背包总的承载重量是 Wkg。现在我们有 n 个物品,每个物品的重量不等,并且不可分割。现在期望选择几件物品,装载到背包中。在不超过背包所能装载重量的前提下,如何让背包中物品的总重量最大?
在贪心算法那一节,有一个类似的例子,不过那里讲的物品是可以分割的,可以装某个物品的一部分到背包里面。这里物品是不可分割的,要么装要么不装,所以叫 0-1 背包问题。显然,这个问题已经无法通过贪心算法来解决了。用回溯算法如何解决?
对于每个物品来说,都有两种选择,装进背包或者不装进背包。对于 n 个物品来说,总的装法就有 2^n 种,去掉总重量超过 Wkg 的,从剩下的装法中选择总重量最接近 Wkg 的。不过,如何才能不重复地穷举出这 2^n 种装法呢?
这里就可以用回溯的方法。把物品依次排列,整个问题就分解为了 n 个阶段,每个阶段对应一个物品怎么选择。先对第一个物品进行处理,选择装进去或者不装进去,然后再递归地处理剩下的物品。
这里还稍微用到了一点搜索剪枝的技巧,就是当发现已经选择的物品的重量超过 Wkg 之后,就停止继续探测剩下的物品。
js
let maxW = Number.MIN_VALUE;
/**
* 0-1 背包
*
* @param {*} i 当前物品标号
* @param {*} currentW 当前的重量
* @param {*} items 每个物品的重量
* @param {*} W 背包承载的重量
* @returns
*/
function findMaxW(i, currentW, items, W) {
// currentW == w 表示装满了; i == items.length - 1 表示已经考察完所有的物品
if (currentW === W || i === items.length - 1) {
if (currentW > maxW) maxW = currentW;
return;
}
// 不装该物品
findMaxW(i + 1, currentW, items, W);
if (currentW + items[i] < W) {
// 装上该物品
findMaxW(i + 1, currentW + items[i], items, W);
}
}
findMaxW(0, 0, [10, 23, 45, 45, 78, 66, 99, 99, 42], 300);
console.log(maxW); // 299
正则表达式
再看看正则表达式的匹配。平常开发中,应该都用过正则表达式。实际上,正则表达式里最重要的一种思想就是回溯。
正则表达式中,最重要的就是通配符,它可以表达非常丰富的语义。为了方便,假设正则表达式中只包含“ * ”和“ ? ”这两种通配符,并且对这两个通配符的语义稍微做些改变:
- “ * ”匹配任意多个(大于等于 0 个)任意字符;
- “ ? ”匹配零个或者一个任意字符。
依次考察正则表达式中的每个字符。
如果遇到非通配符,就直接跟文本的字符进行匹配,如果相同,则继续往下处理;如果不同,则回溯。
如果遇到特殊字符的时候,就有多种处理方式了。也就是所谓的岔路口,比如“ * ”有多种匹配方案,可以匹配任意个文本串中的字符,我们就先随意的选择一种匹配方案,然后继续考察剩下的字符。如果中途发现无法继续匹配下去了,就回到这个岔路口,重新选择一种匹配方案,然后再继续匹配剩下的字符。
js
class Pattern {
constructor(regExp) {
this.matched = false;
this.regExp = regExp.split('');
this.rLength = this.regExp.length;
}
match(text) {
text = text.split('');
let tLength = text.length;
this.matched = false;
this.rmatch(0, 0, text, tLength);
return this.matched;
}
rmatch(tIndex, rIndex, text, tLength) {
if (this.matched) return; // 如果已经匹配了
if (rIndex === this.rLength) { // 正则表达式到结尾了,长度不要减 1
if (tIndex === tLength) { // 字符串到结尾了
this.matched = true;
return;
}
}
if (this.regExp[rIndex] === '*') { // 匹配任意多个
for (let i = 0; i < tLength - tIndex; ++i) {
this.rmatch(tIndex + i, rIndex + 1, text, tLength);
}
} else if (this.regExp[rIndex] === '?') { // 匹配 0 个或 1 个
this.rmatch(tIndex, rIndex + 1, text, tLength);
this.rmatch(tIndex + 1, rIndex + 1, text, tLength);
} else if (tIndex < tLength && this.regExp[rIndex] === text[tIndex]) { // 纯字符串匹配
this.rmatch(tIndex + 1, rIndex + 1, text, tLength);
}
}
}
let test = new Pattern('aa*cc?');
test.match('aabcc'); // true
test.match('aabbcc'); // true
test.match('aabcc'); // true
test.match('aabccd'); // true
test.match('aabbc'); // false
总结
回溯算法的思想非常简单,大部分情况下,都是用来解决广义的搜索问题,也就是,从一组可能的解中,选择出一个满足要求的解。回溯算法非常适合用递归来实现,在实现的过程中,剪枝操作是提高回溯效率的一种技巧。利用剪枝,我们并不需要穷举搜索所有的情况,从而提高搜索效率。
老是纠结“回溯”是要怎么回?看代码时都绕进去了...,确定好递归的终止条件,穷举所有的可能进行递归,并加以判断语句判断是否满足期望。别跟着递归走。